Mr. Malnar (qua điện thoại): Nghe này, tôi đã phải dán một số poster xung quanh Zagreb vào nửa đêm. Tôi tình cờ thấy một hàng rào được làm từ một số tấm ván có độ cao khác nhau, và tôi đang suy nghĩ về cách tính diện tích lớn nhất của một tấm poster mà tôi có thể đặt vừa hàng rào. Nó có đủ tốt để làm 1 bài cho COCI không?

Cộng sự: Ông đã làm gì vậy?! Dẫu sao thì bài này cũng không phù hợp. Đó là một trick cơ bản với hàng đợi đơn điệu, chúng tôi thậm chí còn dạy điều đó cho học sinh tiểu học trong COCI Camps.

Mr. Malnar: Vậy nếu chúng ta thay đổi nó một chút thì sao? Hãy yêu cầu câu trả lời cho mọi tiền tố hoặc thứ gì đó tương tự, điều đó sẽ đủ khó.

Cộng sự: Bài đó đã được ra vào năm ngoái trong bài CREC ở contest vòng loại của chúng ta. Một bài khá khó, nó được kết hợp với Harbingers trick, nhưng bây giờ mọi người đã thấy nó.

Mr. Malnar: Bạn có chắc là chúng ta không thể làm gì được không?

Cộng sự: Tôi nghĩ rằng chúng ta đã giải quyết tất cả các bài tập với biểu đồ. COCI 2010/2011 (Tabovi), COCI 2015/2016 (Poplava), COCI 2017/2018 (Krov), IOI selection test 2018 (Histogram)...

Mr. Malnar: Nếu biểu đồ là ba chiều thì sao?

Cộng sự: Ừm ...

Bạn được cho một biểu đồ 3D, bao gồm ~n~ khối được đặt cạnh nhau. Khối thứ ~i~ có chiều rộng ~1~ ~m~ , chiều cao ~a_i~ ~m~ và chiều dài ~b_i~ ~m~ . Nói cách khác, từ phía trước, nó trông giống như một biểu đồ với các thanh có độ cao ~a_1,a_2,...,a_n~ và từ trên xuống, nó trông giống như một biểu đồ với các thanh có độ cao ~b_1,b_2,...,b_n~.

Xác định khối có thể tích lớn nhất có thể được đặt bên trong biểu đồ 3D đã cho. Các cạnh của khối đó cần phải song song với các cạnh của các khối tạo nên biểu đồ 3D.

Input

Dòng đầu tiên chứa số nguyên ~n~ mô tả nhiệm vụ.

Dòng thứ ~i~ trong số ~n~ dòng sau chứa các số nguyên ~a_i~ và ~b_i~ ~(1 \le a_i,b_i \le 10^6)~ mô tả nhiệm vụ.

Output

In thể tích khối cần tìm theo đơn vị ~m^3~.

Scoring

• có 10 test có ~1 \le n \le 2000~
• 10 test còn lại có ~1 \le n \le 200000~

Sample 1

Input

5
5 3
4 4
2 1
3 2
1 5

Output

24

Sample 2

Input

6
3 1
2 1
2 2
2 3
1 1
2 2

Output

6

Sample 3

Input

5
15 19
5 6
1 13
3 7
1 2

Output

Note

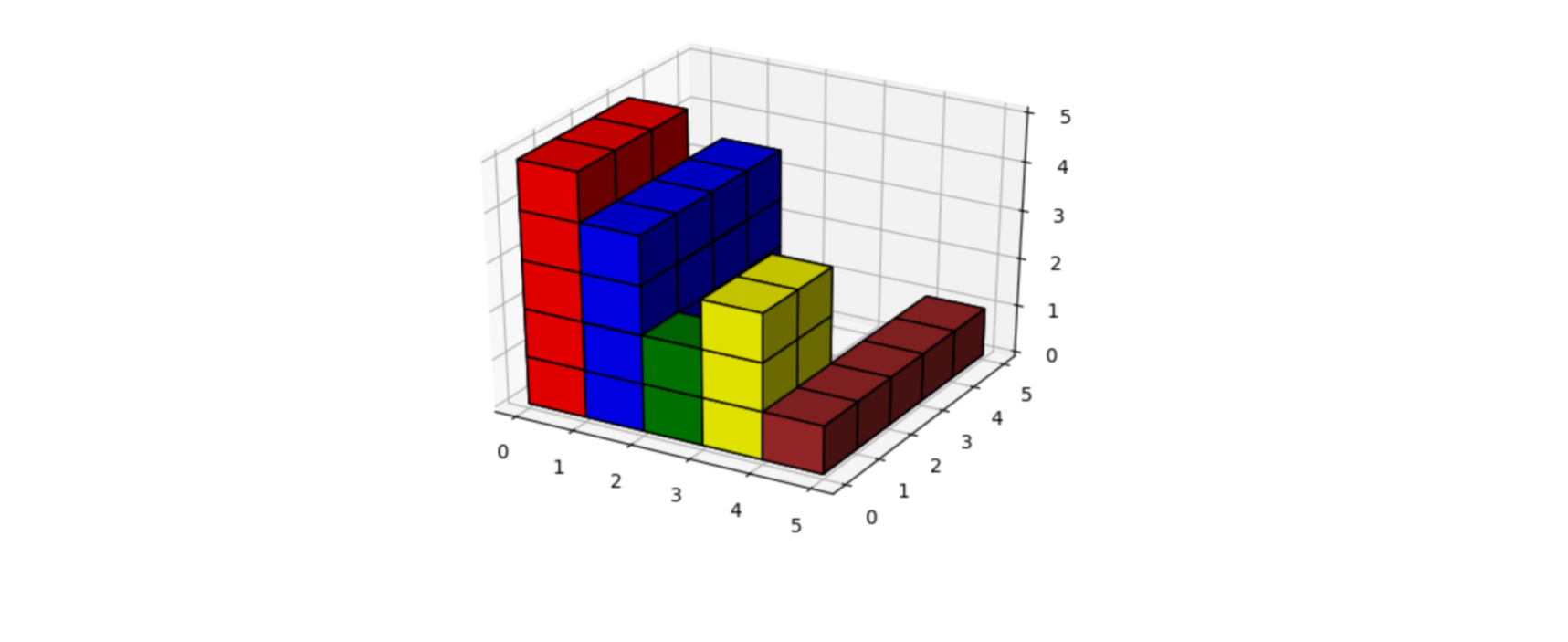
Hình dưới đây cho thấy biểu đồ 3D từ ví dụ đầu tiên. Khối lớn nhất có được bằng cách sử dụng một phần của hai khối đầu tiên, và nó có chiều rộng là ~2m~ , cao ~4m~ và dài ~3m~ . Thể tích của khối là ~2*4*3~ = ~24~ ~m^3~

.