Ở một thành phố nọ có một tòa nhà chọc trời cao có ~n~ tầng. Có ~n~ người đang đợi thang máy ở tầng trệt. Người thứ ~i~ muốn lên tầng ~a_i~. Không có cặp người nào muốn vào cùng một tầng.

Tòa nhà chọc trời có một thang máy đủ rộng cho tất cả mọi người vào, nhưng nó hẹp đến mức hai người không thể đứng cạnh nhau; phải là một người đứng sau người kia.

Mọi người đều vào thang máy nhưng họ chưa nghĩ đến thứ tự phải ra khỏi thang máy! Ban đầu người thứ ~i~ đứng ở vị trí ~i~ nhìn từ cửa thang máy. Nếu có người muốn ra khỏi thang máy thì những người ở phía trước (gần cửa) cũng phải tạm thời ra khỏi thang máy. Khi quay trở lại thang máy, họ có thể tự sắp xếp lại theo ý muốn. Người ở phía sau (xa cửa) người muốn thoát ra sẽ không ra khỏi thang máy.

~\space\space\space\space\space\space\space\space\space\space\space\space\space~

Hình minh họa ở trên thể hiện thứ tự xuất phát của mọi người trong thang máy ở ví dụ đầu tiên. Thang máy ở tầng ~1~, người ở vị trí ~3~ muốn đi ra. Để họ thoát ra, người ở vị trí ~1~ và ~2~ cũng phải thoát ra.

Mirko đang xem tình hình họ đang gặp phải và suy ngẫm. Anh ấy muốn biết sẽ có bao nhiêu lượt ra khỏi thang máy nếu những người quay lại thang máy luôn quay trở lại một cách tối ưu. Nếu một người ra khỏi thang máy nhiều lần thì mỗi lần được tính riêng.

Mirko là một lập trình viên giàu kinh nghiệm và anh ấy có thể giải quyết vấn đề này khá dễ dàng. Niềm vui của anh thật ngắn ngủi vì bên cạnh anh là người bạn Slavko. Slavko đưa ra ~q~ câu hỏi: giả sử nếu người ở vị trí xi không có trong thang máy thì khi đó sẽ có bao nhiêu lối ra?

Mirko quan tâm đến câu trả lời trước câu hỏi đầu tiên của Slavko và sau mỗi câu hỏi. Lưu ý rằng đối với mỗi câu hỏi, tất cả những người ở câu hỏi trước đó không được coi là có trong thang máy. Mirko bắt đầu giải quyết vấn đề nhưng nhanh chóng nhận ra rằng ngay cả đối với anh, việc này cũng không hề dễ dàng. Hãy giúp anh ấy giải quyết vấn đề này!

Lưu ý: Thang máy sẽ luôn di chuyển từ tầng ~1~ đến tầng ~n~ và dừng ở tầng nào có người muốn ra.

Input

• Dòng đầu tiên gồm hai số nguyên không âm ~n~ và ~q~ (~0 \leq q < n \leq 10^5~) số người (hoặc số tầng) và số câu hỏi.
• Dòng thứ hai gồm n số nguyên ~a_i~ (~1 \leq a_i \leq n~, ~a_i \neq a_j~ với mọi ~i \neq j~) là tầng mà người thứ ~i~ sẽ ra khỏi thang máy. Dãy số ~a_i~ là một hoán vị.
• Dòng thứ ba gồm ~q~ số nguyên ~x_i~ (~1 \leq x_i \leq n~, ~x_i \neq x_j~ với mọi ~i \neq j~) mô tả câu hỏi của Slavko.

Output

Trong một dòng, đưa ra ~q+1~ số nguyên, trong đó số thứ i là câu trả lời cho câu hỏi thứ ~i-1~.

Scoring

1. ~n, q \leq 100~ (16 điểm)

2. ~n, q \leq 10^3~ (19 điểm)

3. ~q = 0~ (29 điểm)

4. Không có ràng buộc gì thêm (46 điểm)

Sample Input 1

5 2
3 4 1 2 5
3 2

Sample Output 1

9 6 4

Sample Input 2

7 0
4 5 2 1 6 3 7

Sample Output 2

13

Sample Input 3

3 2
3 1 2
1 2

Sample Output 3

5 2 1

Explanation

Ở ví dụ thứ nhất:

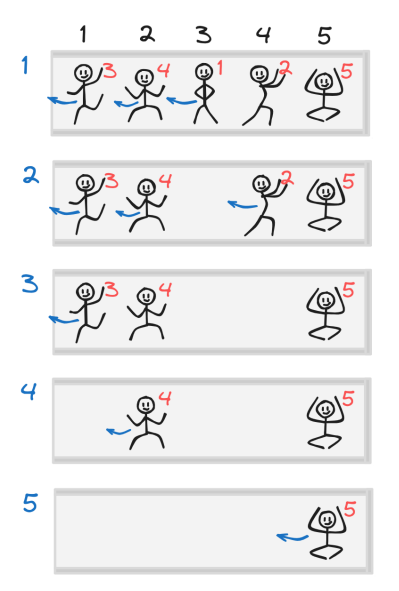
• Thang máy ở tầng một, người ở vị trí số ~3~ muốn đi ra. Tuy nhiên, để thoát ra, người ở vị trí ~1~ và ~2~ phải thoát ra trước và quay trở lại thang máy ở vị trí cũ.
• Sau đó, lên tầng ~2~, người ở vị trí ~4~ muốn thoát ra. Một lần nữa, người ở vị trí ~1~ và ~2~ phải thoát ra trước và quay trở lại thang máy ở vị trí cũ.
• Sau đó, lên tầng ~3~, người ở vị trí số ~1~ ra khỏi thang máy, không cần thêm ai ra khỏi thang máy.
• Sau đó, lến tầng ~4~, người ở vị trí số ~2~ ra khỏi thang máy mà không cần thêm ai khác phải ra khỏi thang máy.
• Và cuối cùng, đến tầng ~5~, người ở vị trí số ~5~ bước ra khỏi thang máy. Tổng cộng có ~3 + 3 + 1 + 1 + 1 = 9~ lượt ra từ thang máy.