Silvia đang ở ga xe lửa Milano Centrale và cô nhận thấy nhà ga có rất nhiều sân ga. Cô nghĩ rằng có quá nhiều thứ nên cô quyết định kiểm tra xem thực sự cần bao nhiêu thứ trong số đó.

Silvia cũng nhận thấy một sự thật thú vị ở trạm này: lịch trình đến và đi được lặp lại hai ngày một lần, ngoài ra, lịch trình sao cho tất cả ~n~ chuyến tàu đến ga vào một ngày và rời ga vào ngày kia. Lưu ý rằng theo cách này sẽ không có chuyến tàu nào khởi hành trước khi tất cả các chuyến tàu đã đến.

Sân ga ở ga đủ dài để tất cả n đoàn tàu có thể xếp hàng nối tiếp nhau trên cùng một sân ga. Tuy nhiên, nếu tàu ~x~ vào sân ga trước rồi đến tàu ~y~, thì tàu ~x~ không thể rời sân ga trước tàu ~y~.

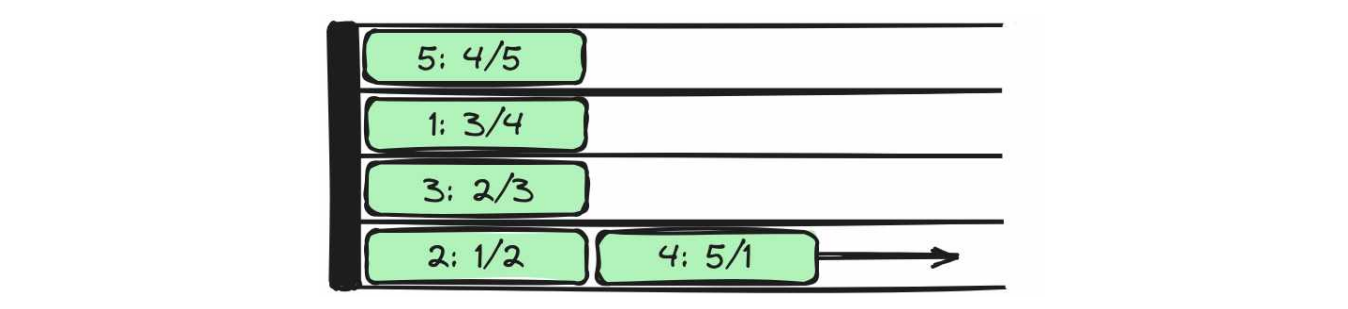
Hình minh họa cho thấy lịch trình tàu có thể có trên các sân ga trong ví dụ thứ hai. Nhãn trên tàu "~i~: ~a_i/b_i~" cho thấy tàu thứ ~i~ đến trạm thứ ~a_i~ vào ngày đầu tiên và rời trạm thứ ~b_i~ vào ngày thứ hai. Tàu ~(2: 1/2)~ không thể rời sân ga trước tàu ~(4: 5/1)~.

Silvia quan tâm đến số lượng sân ga tối thiểu cần thiết để tất cả các đoàn tàu có thể xếp hàng trên sân ga mà không có khả năng tàu không thể rời sân ga vì có một đoàn tàu phía trước vẫn chưa rời bến.

Input

• Dòng đầu tiên gồm số nguyên n (~1 \leq n \leq 2 \times 10^5~) là số tàu.
• Dòng thứ hai gồm n số nguyên ~a_i~ (~1 \leq a_i \leq n~, ~a_i \neq a_j~ với mọi ~i \neq j~) là thứ tự mà tàu ~i~ đến trạm vào ngày đầu tiên. Dãy số ~(a_i)~ là một hoán vị.
• Dòng thứ hai gồm n số nguyên ~b_i~ (~1 \leq b_i \leq n~, ~b_i \neq b_j~ với mọi ~i \neq j~) là thứ tự mà tàu ~i~ rời trạm vào ngày thứ hai. Dãy số ~(b_i)~ là một hoán vị.

Output

Trong một dòng duy nhất, đưa ra số sân ga cần nhỏ nhất.

Scoring

1. ~n \leq 10~ (21 điểm)

2. Số sân ga cần nhỏ nhất hoặc là ~1~ hoặc là ~2~ (18 điểm)

3. ~n \leq 10^3~ (31 điểm)

4. Không có ràng buộc gì thêm (40 điểm)

Sample Input 1

5
3 5 2 4 1
3 2 5 1 4

Sample Output 1

2

Sample Input 2

5
3 1 2 5 4
4 2 3 1 5

Sample Output 2

4

Sample Input 3

3
3 2 1
1 2 3

Sample Output 3

1